Serial to Parallel

Overview

Teaching: 30 min
Exercises: 30 min

Questions

What is the best way to write a parallel code?

How do I parallelise my serial code?

Objectives

Go through practical steps for going from a serial code to a parallel code.

Display Language
Show C	Show Fortran	Show Python

Going from Serial to Parallel

The examples used in the previous sections were perhaps not the most realistic. In this section we will look at a more complete code and take it from serial to parallel in a couple of steps.

The exercises and solutions are based on a code that solves the Poisson’s equation using an iterative method. In this case the equation describes how heat diffuses in a metal stick. In the simulation the stick is split into small sections with a constant temperature. At one end the amount of heat is set to 10 and at the other to 0. The code applies steps that bring each point closer to a solution untill it reaches an equilibrium.

/* A serial code for Poisson equation 
 * This will apply the diffusion equation to an initial state
 * untill an equilibrium state is reached. */

/* contact seyong.kim81@gmail.com for comments and questions */


#include <stdio.h>
#include <math.h>
#include <stdlib.h>

#define GRIDSIZE 10


/* Apply a single time step */
double poisson_step( 
     float *u, float *unew, float *rho,
     float hsq, int points
   ){
   double unorm;
 
   // Calculate one timestep
   for( int i=1; i <= points; i++){
      float difference = u[i-1] + u[i+1];
      unew[i] = 0.5*( difference - hsq*rho[i] );
   }
 
   // Find the difference compared to the previous time step
   unorm = 0.0;
   for( int i = 1;i <= points; i++){
      float diff = unew[i]-u[i];
      unorm +=diff*diff;
   }
 
   // Overwrite u with the new value
   for( int i = 1;i <= points;i++){
      u[i] = unew[i];
   }
 
   return unorm;
}



int main(int argc, char** argv) {

   // The heat energy in each block
   float u[GRIDSIZE+2], unew[GRIDSIZE+2], rho[GRIDSIZE+2];
   int i;
   float h, hsq;
   double unorm, residual;

   /* Set up parameters */
   h = 0.1;
   hsq = h*h;
   residual = 1e-5;
 
   // Initialise the u and rho field to 0 
   for(i=0; i <= GRIDSIZE+1; i++) {
      u[i] = 0.0;
      rho[i] = 0.0;
   }

   // Create a start configuration with the heat energy
   // u=10 at the x=0 boundary
   u[0] = 10.0;
 
   // Run iterations until the field reaches an equilibrium
   // and no longer changes
   for( i=0; i<10000; i++ ) {
     unorm = poisson_step( u, unew, rho, hsq, GRIDSIZE );
     printf("Iteration %d: Residue %g\n", i, unorm);
     
     if( sqrt(unorm) < sqrt(residual) ){
       break;
     }
   }
 
   printf("Run completed with residue %g\n", unorm);

}

! A serial code for Poisson equation 
! This will apply the diffusion equation to an initial state
! untill an equilibrium state is reached. 

! contact seyong.kim81@gmail.com for comments and questions 
      
program poisson

   implicit none

   integer, parameter :: GRIDSIZE=10
   integer i

   real u(0:(GRIDSIZE+1)), unew(0:(GRIDSIZE+1))
   real rho(0:(GRIDSIZE+1))
   real h, hsq
   double precision unorm, residual

   ! Set up parameters
   h = 0.1
   hsq = h*h
   residual = 1e-5

   ! Initialise the u and rho field to 0 
   do i = 0, GRIDSIZE+1
      u(i) = 0.0
      rho(i) = 0.0
   enddo

   ! Create a start configuration with the field
   ! u=10 at the x=0 boundary
   u(0) = 10.0

   ! Run iterations until the field reaches an equilibrium and
   ! no longer changes
   do 

      call poisson_step(u, unew, rho, GRIDSIZE, hsq, unorm)
      write(6,*) 'Iteration', i, ', residue', unorm

      if ( sqrt(unorm) <= sqrt(residual) ) then
         exit
      end if

   enddo

   write(6,*) 'Run completed with residue ', unorm

end

! Apply a single time step
subroutine poisson_step(u, unew, rho, GRIDSIZE, hsq, unorm)

   implicit none

   integer, intent(in) :: GRIDSIZE
   real, intent(inout), dimension (0:(GRIDSIZE+1)) :: u, unew
   real, intent(in), dimension (0:(GRIDSIZE+1)) :: rho
   real, intent(in) :: hsq
   double precision, intent(out) :: unorm
   integer i, j
   
   ! Calculate one timestep
   do i = 1, GRIDSIZE
      unew(i) = 0.25*(u(i-1)+u(i+1)- hsq*rho(i))
   enddo

   ! Find the difference compared to the previous time step
   unorm = 0.0
   do i = 1, GRIDSIZE
      unorm = unorm + (unew(i)-u(i))*(unew(i)-u(i))
   enddo

   ! Overwrtie u with the new value
   do i = 1, GRIDSIZE
      u(i) = unew(i)
   enddo
end

"""a serial code for Poisson equation
   contact seyong.kim81@gmail.com for comments and questions
"""

import numpy as np
import math

def poisson_step(GRIDSIZE, u, unew, rho, hsq):

    # Calculate one timestep
    for j in range(1, GRIDSIZE+1):
        for i in range(1, GRIDSIZE+1):
            difference = u[j][i-1] + u[j][i+1] + u[j-1][i] + u[j+1][i]
            unew[j][i] = 0.25*(difference - hsq*rho[j][i])

    # Find the difference compared to the previous time step
    unorm = 0.0
    for j in range(1, GRIDSIZE+1):
        for i in range(1, GRIDSIZE+1):
            diff = unew[j][i] - u[j][i]
            unorm +=diff*diff

    # Overwrite u with the new field
    for j in range(1, GRIDSIZE+1):
        for i in range(1, GRIDSIZE+1):
            u[j][i] = unew[j][i]

    return unorm

GRIDSIZE = 10

u = np.zeros((GRIDSIZE+2, GRIDSIZE+2))
unew = np.zeros((GRIDSIZE+2, GRIDSIZE+2))
rho = np.zeros((GRIDSIZE+2, GRIDSIZE+2))

# Set up parameters
h = 0.1
hsq = h*h
residual = 1e-5

# Initialise the u and rho field to 0
for j in range(GRIDSIZE+2):
    for i in range(GRIDSIZE+2):
        u[j][i] = 0.0
        rho[j][i] = 0.0

# Create a start configuration with the field
# u=10 at x=0
for j in range(GRIDSIZE+2):
    u[j][0] = 10.0

# Run iterations until the field reaches an equilibrium
for i in range(10000):
    unorm = poisson_step(GRIDSIZE, u, unew, rho, hsq)
    print("Iteration {:d}: Residue {:g}".format(i, unorm))

    if math.sqrt(unorm) < math.sqrt(residual):
        break

print("Run completed with residue", unorm)

Parallel Regions

The first step is to identify parts of the code that can be written in parallel. Go through the algorithm and decide for each region if the data can be partitioned for parallel execution, or if certain tasks can be separated and run in parallel.

Can you find large or time consuming serial regions? The sum of the serial regions gives the minimum amount of time it will take to run the program. If the serial parts are a significant part of the algorithm, it may not be possible to write an efficient parallel version. Can you replace the serial parts with a different, more parallel algorithm?

Parallel Regions

Identify any parallel and serial regions in the code. What would be the optimal parallelisation strategy?

Solution

The loops over space can be run in parallel. There are parallisable loops in:

the setup, when initialising the fields.

the calculation of the time step, unew.

the difference, unorm.

overwriting the field u.

writing the files could be done in parallel.

The best strategy would seem to be parallelising the loops. This will lead to a domain decomposed implementation with the elements of the fields u and rho divided across the ranks.

Communication Patterns

If you decide it’s worth your time to try to parallelise the problem, the next step is to decide how the ranks will share the tasks or the data. This should be done for each region separately, but taking into account the time it would take to reorganise the data if you decide to change the pattern between regions.

The parallelisation strategy is often based on the underlying problem the algorithm is dealing with. For example, in materials science it makes sense to decompose the data into domains by splitting the physical volume of the material.

Most programs will use the same pattern in every region. There is a cost to reorganising data, mostly having to do with communicating large blocks between ranks. This is really only a problem if done in a tight loop, many times per second.

Communications Patterns

How would you divide the data between the ranks? When does each rank need data from other ranks? Which ranks need data from which other ranks?

Solution

Only one of the loops requires data from the other ranks, and these are only nearest neighbours.

Parallelising the loops would actually be the same thing as splitting the physical volume. Each iteration of the loop accesses one element in the rho and uner fields and four elements in the u field. The u field needs to be communicated if the value is stored on a different rank.

There is also a global reduction for calculating unorm. Every node needs to know the result.

Set Up Tests

Write a set of tests for the function you are planning to edit. The tests should be sufficient to make sure each function performs correctly in any situation when all tests pass. You should test all combinations of different types of parameters and preferably use random input. Here the habit of modular programming is very useful. When the functions are small and have a small amount of possible input types, they are easy to test.

Automated Testing

There are automated unit testing frameworks for almost any programming language. Automated testing greatly simplifies the workflow of running your tests and verifying that the entire program is correct. The program here is still relatively simple, we are testing a single function, so writing a main function with a test case is enough.

Check out the cmocka or cunit unit testing frameworks.

Check out the fortran-unit-test unit testing frameworks.

Write a Test

Change the main function of the poisson code to check that the poisson_step function produces the correct result. Test at least the output after 1 step and after 10 steps.

What would you need to check to make sure the function is absolutely correct?

Solution

int main(int argc, char** argv) {

  int i, j;
  float u[GRIDSIZE+2], unew[GRIDSIZE+2], rho[GRIDSIZE+2];
  float h, hsq;
  double unorm;

  /* Set up parameters */
  h = 0.1;

  /* Run Setup */
  hsq = h*h;

  // Initialise the u and rho field to 0 
  for( int i=0; i <= GRIDSIZE+1; i++ ) {
     u[i] = 0.0;
     rho[i] = 0.0;
  }

  // Test a configuration with u=10 at x=0 boundary
  u[0] = 10;

  // Run a single iteration first
  unorm = poisson_step( u, unew, rho, hsq, GRIDSIZE );

  if( unorm == 25 ){
    printf("TEST SUCCEEDED after 1 iteration\n");
  } else {
    printf("TEST FAILED after 1 iteration\n");
    printf("Norm %g\n", unorm);
  }

  // Run 9 more iterations for a total of 10
  for( i=1; i<10; i++)
    unorm = poisson_step( u, unew, rho, hsq, GRIDSIZE );

  if( fabs(unorm - 0.463676) < 1e-6 ){
    printf("TEST SUCCEEDED after 10 iteration\n");
  } else {
    printf("TEST FAILED after 10 iteration\n");
    printf("Norm %g\n", unorm);
  }

}

Solution

Here we create a module for the poisson solver, including only the subroutine for performing a single step.

program poisson

  implicit none

  integer, parameter :: GRIDSIZE=10
  integer i

  real u(0:(GRIDSIZE+1)), unew(0:(GRIDSIZE+1))
  real rho(0:(GRIDSIZE+1))
  real h, hsq
  double precision unorm, difference

  ! Set up parameters
  h = 0.1
  hsq = h*h

  ! Initialise the u and rho field to 0 
  do i = 0, GRIDSIZE+1
      u(i) = 0.0
      rho(i) = 0.0
  enddo
  

  ! Test a configuration with u=10 at x=0 boundary
  u(0) = 10

  ! Run a single iteration of the poisson solver
  call poisson_step( u, unew, rho, GRIDSIZE, hsq, unorm )
  
  if (unorm == 25) then
     write(6,*) "PASSED after 1 step"
  else
     write(6,*) "FAILED after 1 step"
     write(6,*) unorm
  end if

  ! Run 9 more iterations for a total of 10
  do i = 1, 10
     call poisson_step( u, unew, rho, GRIDSIZE, hsq, unorm )
  end do

  difference = unorm - 0.40042400360107422
  if (difference*difference < 1e-16) then
     write(6,*) "PASSED after 10 steps"
  else
     write(6,*) "FAILED after 10 steps"
     write(6,*) unorm
  end if

end

Solution

import numpy as np

GRIDSIZE = 10

u = np.zeros((GRIDSIZE+2, GRIDSIZE+2))
unew = np.zeros((GRIDSIZE+2, GRIDSIZE+2))
rho = np.zeros((GRIDSIZE+2, GRIDSIZE+2))

# Set up parameters
h = 0.1

# Run Setup
hsq = h**2

# Initialise the u and rho field to 0
for j in range(GRIDSIZE+2):
    for i in range(GRIDSIZE+2):
        u[j][i] = 0.0
        rho[j][i] = 0.0

# Test a configuration with u=10 at x=1 and y=1
u[1][1] = 10

# Run a single iteration first
unorm = poisson_step(GRIDSIZE, u, unew, rho, hsq)

if unorm == 112.5:
    print("TEST SUCCEEDED after 1 iteration")
else:
    print("TEST FAILED after 1 iteration")

for i in range(1, 10):
    unorm = poisson_step(GRIDSIZE, u, unew, rho, hsq)

if abs(unorm - 0.208634816) < 1e-6:
    print("TEST SUCCEEDED after 10 iteration")
else:
    print("TEST FAILED after 10 iteration")

Make the test work in parallel

Modify the test so that it runs correctly with multiple MPI ranks. The tests should succeed when run with a single rank and fail with any other number of ranks.

At this point you will need to decide how the data is arranged before the function is called. Will it be distributed before the function is called, or will you split and distribute the data each time the function is called? In this case the poisson_step function is called many times and splitting the data up each time would take a lot of time, so we assume it is distributed before the function call.

Let’s split the outer loop, indexed with j, across the ranks. Each rank will have a slice of GRIDSIZE/n_ranks points in the j direction. Modify the main function so that it works properly with MPI and each rank only initializes its own data.

Solution

int main(int argc, char** argv) {

   int i, j;
   float *u, *unew, *rho;
   float h, hsq;
   double unorm, residual;
   int n_ranks, rank, my_j_max;

   // First call MPI_Init
   MPI_Init(&argc, &argv);

   /* Find the number of x-slices calculated by each rank */
   /* The simple calculation here assumes that GRIDSIZE is divisible by n_ranks */
   MPI_Comm_rank(MPI_COMM_WORLD, &rank);
   MPI_Comm_size(MPI_COMM_WORLD, &n_ranks);
   my_j_max = GRIDSIZE/n_ranks;


   /* Allocate the field u and a temporary variable unew.
    * The number of points in the real volume is GRIDSIZE.
    * Reserve space also for boundary conditions. */
   u    = malloc( (my_j_max+2)*sizeof(float*) );
   unew = malloc( (my_j_max+2)*sizeof(float*) );
   rho  = malloc( (my_j_max+2)*sizeof(float*) );


   /* Set up parameters */
   h = 0.1;
 
   /* Run Setup */
   hsq = h*h;

   // Initialise the u and rho field to 0 
   for( int i=0; i <= my_j_max+1; i++ ) {
      u[i] = 0.0;
      rho[i] = 0.0;
   }

   // Test a configuration with u=10 at x=0 boundary
   // The actual x coordinate is my_j_max*rank + x
   // meaning that x=1 is on rank 0
   if( rank == 0 )
      u[0] = 10;
    
   // Run a single iteration first
   unorm = poisson_step( u, unew, rho, hsq, my_j_max );
 
  if( unorm == 25 ){
    printf("TEST SUCCEEDED after 1 iteration\n");
  } else {
    printf("TEST FAILED after 1 iteration\n");
    printf("Norm %g\n", unorm);
  }

  for( i=1; i<10; i++)
    unorm = poisson_step( u, unew, rho, hsq, my_j_max );

  if( fabs(unorm - 0.463676) < 1e-6 ){
    printf("TEST SUCCEEDED after 10 iteration\n");
  } else {
    printf("TEST FAILED after 10 iteration\n");
    printf("Norm %g\n", unorm);
  }

  
   /* Free the allocated fields */
   free(u);
   free(unew);
   free(rho);

   // Call finalize at the end
   return MPI_Finalize();
}

Notice that we now allocate space for the entire lattice on each node. Since we haven’t touched the poisson_step function, it will still try to update all the points and access all the memory. Allocating only the part our rank needs would produce a segmentation fault.

Solution

program poisson

  implicit none
  include "mpif.h" 

  integer, parameter :: GRIDSIZE=10
  ! We don't know the number of ranks yet, so we
  ! allocate these arrays later
  real, allocatable :: u(:), unew(:)
  real, allocatable :: rho(:)
  integer i
  integer my_rank, n_ranks, ierr
  integer my_j_max

  real h, hsq
  double precision unorm, difference

  ! Initialize MPI
  call MPI_Init(ierr)

  ! Get my rank and the number of ranks
  call MPI_Comm_rank(MPI_COMM_WORLD, my_rank, ierr)
  call MPI_Comm_size(MPI_COMM_WORLD, n_ranks, ierr)

  ! Find the number of x-slices calculated by each rank
  ! The simple calculation here assumes that GRIDSIZE is divisible by n_ranks
  my_j_max = GRIDSIZE/n_ranks;

  ! Now allocate the fields
  real u(0:(my_j_max+1)), unew(0:(my_j_max+1))
  real rho(0:(my_j_max+1))

  ! Set up parameters
  h = 0.1
  hsq = h*h

  ! Initialise the u and rho field to 0 
  do i = 0, my_j_max+1
      u(i) = 0.0
      rho(i) = 0.0
  enddo

  ! Test a configuration with u=10 at x=0 boundary
  if (my_rank == 0) then	
    u(0) = 10
  end if

  ! Run a single iteration of the poisson solver
  call poisson_step( u, unew, rho, my_j_max, hsq, unorm )
  
  if (unorm == 25) then
     write(6,*) "PASSED after 1 step"
  else
     write(6,*) "FAILED after 1 step"
     write(6,*) unorm
  end if

  ! Run 9 more iterations for a total of 10
  do i = 1, 10
     call poisson_step( u, unew, rho, my_j_max, hsq, unorm )
  end do

  difference = unorm - 0.40042400360107422
  if (difference*difference < 1e-16) then
     write(6,*) "PASSED after 10 steps"
  else
     write(6,*) "FAILED after 10 steps"
     write(6,*) unorm
  end if

  ! Call MPI_Finalize at the end
  call MPI_Finalize(ierr)

end

Solution

from mpi4py import MPI
import numpy as np

GRIDSIZE = 10

u = np.zeros((GRIDSIZE+2, GRIDSIZE+2))
unew = np.zeros((GRIDSIZE+2, GRIDSIZE+2))
rho = np.zeros((GRIDSIZE+2, GRIDSIZE+2))

# Find the number of x-slices calculated by each rank
# The simple calculation here assumes that GRIDSIZE is divisible by n_ranks
rank = MPI.COMM_WORLD.Get_rank()
n_ranks = MPI.COMM_WORLD.Get_size()
my_j_max = GRIDSIZE // n_ranks

# Set up parameters
h = 0.1

# Run Setup
hsq = h**2

# Initialise the u and rho field to 0
for j in range(my_j_max+2):
    for i in range(GRIDSIZE+2):
        u[j][i] = 0.0
        rho[j][i] = 0.0

# Start form a configuration with u=10 at x=1 and y=1
# The actual x coordinate is my_j_max*rank + x
# meaning that x=1 is on rank 0
if rank == 0:
    u[1][1] = 10

# Run a single iteration first
unorm = poisson_step(GRIDSIZE, u, unew, rho, hsq)

if unorm == 112.5:
    print("TEST SUCCEEDED after 1 iteration")
else:
    print("TEST FAILED after 1 iteration")
    print("Norm", unorm)

for i in range(1, 10):
    unorm = poisson_step(GRIDSIZE, u, unew, rho, hsq)

if abs(unorm - 0.208634816) < 1e-6:
    print("TEST SUCCEEDED after 10 iteration")
else:
    print("TEST FAILED after 10 iteration")
    print("Norm", unorm)

Write a Parallel Function Thinking About a Single Rank

In the message passing framework, all ranks execute the same code. When writing a parallel code with MPI, you should think of a single rank. What does this rank need to to and what information does it need to do it?

Communicate data in the simplest possible way just after it’s created or just before it’s needed. Use blocking or non-blocking communication, whichever you feel is simpler. If you use non-blocking functions, call wait immediately.

The point is to write a simple code that works correctly. You can optimise later.

Parallel Execution

First, just implement a single step. Write a program that performs the iterations from j=rank*(GRIDSIZE/n_ranks) to j=(rank+1)*(GRIDSIZE/n_ranks). For this, you should not need to communicate the field u. You will need a reduction.

After this step the first test should succeed and the second test should fail.

Solution

double poisson_step( 
    float *u, float *unew, float *rho,
    float hsq, int points
  ){
  /* We will calculate unorm separately on each rank. It needs to be summed up at the end*/
  double unorm;
  /* This will be the sum over all ranks */
  double global_unorm;

  // Calculate one timestep
  for( int i=1; i <= points; i++){
     float difference = u[i-1] + u[i+1];
     unew[i] = 0.5*( difference - hsq*rho[i] );
  }

  // Find the difference compared to the previous time step
  unorm = 0.0;
  for( int i = 1;i <= points; i++){
     float diff = unew[i]-u[i];
     unorm +=diff*diff;
  }

  // Use Allreduce to calculate the sum over ranks
  MPI_Allreduce( &unorm, &global_unorm, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD );

  // Overwrite u with the new field
  for( int i = 1;i <= points;i++){
     u[i] = unew[i];
  }

  // Return the sum over all ranks
  return global_unorm;
}

Solution

subroutine poisson_step(u, unew, rho, GRIDSIZE, hsq, unorm)

   implicit none
   include "mpif.h"

   integer, intent(in) :: GRIDSIZE
   real, intent(inout), dimension (0:(GRIDSIZE+1)) :: u, unew
   real, intent(in), dimension (0:(GRIDSIZE+1)) :: rho
   real, intent(in) :: hsq
   double precision local_unorm
   double precision, intent(out) :: unorm
   integer my_j_max, n_ranks
   integer ierr, i
   
   ! Calculate one timestep
   do i = 1, GRIDSIZE
     unew(i) = 0.5*(u(i-1)+u(i+1)- hsq*rho(i))
   enddo

   ! Find the difference compared to the previous time step
   local_unorm = 0.0
   do i = 1, GRIDSIZE
       local_unorm = local_unorm + (unew(i)-u(i))*(unew(i)-u(i))
   enddo

   call MPI_Allreduce( local_unorm, unorm, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD, ierr )

   ! Overwrite u with the new field
   do i = 1, GRIDSIZE
       u(i) = unew(i)
   enddo

end subroutine poisson_step

Solution

def poisson_step(GRIDSIZE, u, unew, rho, hsq):

    # Find the number of x-slices calculated by each rank
    # The simple calculation here assumes that GRIDSIZE is divisible by n_ranks
    rank = MPI.COMM_WORLD.Get_rank()
    n_ranks = MPI.COMM_WORLD.Get_size()
    my_j_max = GRIDSIZE // n_ranks

    # Calculate one timestep
    for j in range(1, my_j_max+1):
        for i in range(1, GRIDSIZE+1):
            difference = u[j][i-1] + u[j][i+1] + u[j-1][i] + u[j+1][i]
            unew[j][i] = 0.25 * (difference - hsq * rho[j][i])

    # Find the difference compared to the previous time step
    unorm = 0.0
    for j in range(1, my_j_max+1):
        for i in range(1, GRIDSIZE+1):
            diff = unew[j][i] - u[j][i]
            unorm += diff**2

    # Use Allreduce to calculate the sum over ranks
    global_unorm = MPI.COMM_WORLD.allreduce(unorm, op=MPI.SUM)

    # Overwrite u with the new field
    for j in range(1, my_j_max+1):
        for i in range(1, GRIDSIZE+1):
            u[j][i] = unew[j][i]

    # Return the sum over all ranks
    return global_unorm

Communication

Add in the nearest neighbour communication. The second test should then succeed.

Solution

Each rank needs to send the values at u[1] down to rank-1 and the values at u[my_j_max] to rank+1. There needs to be an exception for the first and the last rank.

double poisson_step( 
  float *u, float *unew, float *rho,
  float hsq, int points
){
  double unorm, global_unorm;
  float sendbuf, recvbuf;
  MPI_Status mpi_status;
  int rank, n_ranks;
 
  /* Find the number of x-slices calculated by each rank */
  /* The simple calculation here assumes that GRIDSIZE is divisible by n_ranks */
  MPI_Comm_rank(MPI_COMM_WORLD, &rank);
  MPI_Comm_size(MPI_COMM_WORLD, &n_ranks);
   
  // Calculate one timestep
  for( int i=1; i <= points; i++){
     float difference = u[i-1] + u[i+1];
     unew[i] = 0.5*( difference - hsq*rho[i] );
  }

  // Find the difference compared to the previous time step
  unorm = 0.0;
  for( int i = 1;i <= points; i++){
     float diff = unew[i]-u[i];
     unorm +=diff*diff;
  }
 
  // Use Allreduce to calculate the sum over ranks
  MPI_Allreduce( &unorm, &global_unorm, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD );
 
  // Overwrite u with the new field
  for( int i = 1;i <= points;i++){
     u[i] = unew[i];
  }
 
  // The u field has been changed, communicate it to neighbours
  // With blocking communication, half the ranks should send first
  // and the other half should receive first
  if ((rank%2) == 1) {
    // Ranks with odd number send first
 
    // Send data down from rank to rank-1
    sendbuf = unew[1];
    MPI_Send(&sendbuf,1,MPI_FLOAT,rank-1,1,MPI_COMM_WORLD);
    // Receive dat from rank-1
    MPI_Recv(&recvbuf,1,MPI_FLOAT,rank-1,2,MPI_COMM_WORLD,&mpi_status);
    u[0] = recvbuf;
     
    if ( rank != (n_ranks-1)) {
      // Send data up to rank+1 (if I'm not the last rank)
      MPI_Send(&u[points],1,MPI_FLOAT,rank+1,1,MPI_COMM_WORLD);
      // Receive data from rank+1
      MPI_Recv(&u[points+1],1,MPI_FLOAT,rank+1,2,MPI_COMM_WORLD,&mpi_status);
    }
  
  } else {
    // Ranks with even number receive first
 
    if (rank != 0) {
      // Receive data from rank-1 (if I'm not the first rank)
      MPI_Recv(&u[0],1,MPI_FLOAT,rank-1,1,MPI_COMM_WORLD,&mpi_status);
      // Send data down to rank-1
      MPI_Send(&u[1],1,MPI_FLOAT,rank-1,2,MPI_COMM_WORLD);
    }
 
    if (rank != (n_ranks-1)) {
      // Receive data from rank+1 (if I'm not the last rank)
      MPI_Recv(&u[points+1],1,MPI_FLOAT,rank+1,1,MPI_COMM_WORLD,&mpi_status);
      // Send data up to rank+1
      MPI_Send(&u[points],1,MPI_FLOAT,rank+1,2,MPI_COMM_WORLD);
    }
  }
 
  return global_unorm;
}

Solution

Each rank needs to send the values at u(1) down to rank-1 and the values at u(my_j_max) to rank+1. There needs to be an exception for the first and the last rank.

subroutine poisson_step(u, unew, rho, GRIDSIZE, hsq, unorm)

   implicit none
   include "mpif.h"

   integer, intent(in) :: GRIDSIZE
   real, intent(inout), dimension (0:(GRIDSIZE+1)) :: u, unew
   real, intent(in), dimension (0:(GRIDSIZE+1)) :: rho
   real, intent(in) :: hsq
   double precision local_unorm
   double precision, intent(out) :: unorm
   integer status(MPI_STATUS_SIZE)
   integer n_ranks, my_rank
   integer ierr, i
   
   ! Find the number of x-slices calculated by each rank
   ! The simple calculation here assumes that GRIDSIZE is divisible by n_ranks
   call MPI_Comm_rank(MPI_COMM_WORLD, my_rank, ierr)
   call MPI_Comm_size(MPI_COMM_WORLD, n_ranks, ierr)

   ! Calculate one timestep
   do i = 1, GRIDSIZE
     unew(i) = 0.5*(u(i-1)+u(i+1)- hsq*rho(i))
   enddo

   ! Find the difference compared to the previous time step
   local_unorm = 0.0
   do i = 1, GRIDSIZE
       local_unorm = local_unorm + (unew(i)-u(i))*(unew(i)-u(i))
   enddo

   call MPI_Allreduce( local_unorm, unorm, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD, ierr )

   ! Overwrite u with the new field
   do i = 1, GRIDSIZE
       u(i) = unew(i)
   enddo

  ! The u field has been changed, communicate it to neighbours
  ! With blocking communication, half the ranks should send first
  ! and the other half should receive first
  if (mod(my_rank,2) == 1) then
      ! Ranks with odd number send first
  
      ! Send data down from my_rank to my_rank-1
      call MPI_Send( u(1), 1, MPI_REAL, my_rank-1, 1, MPI_COMM_WORLD, ierr)
      ! Receive dat from my_rank-1
      call MPI_Recv( u(0), 1, MPI_REAL, my_rank-1, 2, MPI_COMM_WORLD, status, ierr)
  
      if (my_rank < (n_ranks-1)) then
         call MPI_Send( u(GRIDSIZE),   1, MPI_REAL, my_rank+1, 1, MPI_COMM_WORLD, ierr)
         call MPI_Recv( u(GRIDSIZE+1), 1, MPI_REAL, my_rank+1, 2, MPI_COMM_WORLD, status, ierr)
      endif
  
  else
      ! Ranks with even number receive first
  
      if (my_rank > 0) then
         call MPI_Recv( u(0), 1, MPI_REAL, my_rank-1, 1, MPI_COMM_WORLD, status, ierr)
         call MPI_Send( u(1), 1, MPI_REAL, my_rank-1, 2, MPI_COMM_WORLD, ierr)
      endif
  
      if (my_rank < (n_ranks-1)) then
         call MPI_Recv( u(GRIDSIZE+1), 1, MPI_REAL, my_rank+1, 1, MPI_COMM_WORLD, status, ierr)
         call MPI_Send( u(GRIDSIZE),   1, MPI_REAL, my_rank+1, 2, MPI_COMM_WORLD, ierr)
      endif
  endif

end subroutine poisson_step

Solution

Each rank needs to send the values at u(1) down to rank-1 and the values at u(my_j_max) to rank+1. There needs to be an exception for the first and the last rank.

def poisson_step(GRIDSIZE, u, unew, rho, hsq):

    sendbuf = np.zeros(GRIDSIZE)

    # Find the number of x-slices calculated by each rank
    # The simple calculation here assumes that GRIDSIZE is divisible by n_ranks
    rank = MPI.COMM_WORLD.Get_rank()
    n_ranks = MPI.COMM_WORLD.Get_size()
    my_j_max = GRIDSIZE // n_ranks

    # Calculate one timestep
    for j in range(1, my_j_max+1):
        for i in range(1, GRIDSIZE+1):
            difference = u[j][i-1] + u[j][i+1] + u[j-1][i] + u[j+1][i]
            unew[j][i] = 0.25 * (difference - hsq * rho[j][i])

    # Find the difference compared to the previous time step
    unorm = 0.0
    for j in range(1, my_j_max+1):
        for i in range(1, GRIDSIZE+1):
            diff = unew[j][i] - u[j][i]
            unorm += diff**2

    # Use Allreduce to calculate the sum over ranks
    global_unorm = MPI.COMM_WORLD.allreduce(unorm, op=MPI.SUM)

    # Overwrite u with the new field
    for j in range(1, my_j_max+1):
        for i in range(1, GRIDSIZE+1):
            u[j][i] = unew[j][i]

    # The u field has been changed, communicate it to neighbours
    # With blocking communication, half the ranks should send first
    # and the other half should receive first
    if rank % 2 == 1:
        # Ranks with odd number send first

        # Send data down from rank to rank-1
        for i in range(GRIDSIZE):
            sendbuf[i] = unew[1][i+1]
        MPI.COMM_WORLD.send(sendbuf, dest=rank-1, tag=1)

        # Receive dat from rank-1
        recvbuf = MPI.COMM_WORLD.recv(source=rank-1, tag=2)
        for i in range(GRIDSIZE):
            u[0][i+1] = recvbuf[i]

        if rank != (n_ranks-1):
            # Send data up to rank+1 (if I'm not the last rank)
            for i in range(GRIDSIZE):
                sendbuf[i] = unew[my_j_max][i+1]
            MPI.COMM_WORLD.send(sendbuf, dest=rank+1, tag=1)

            # Receive data from rank+1
            recvbuf = MPI.COMM_WORLD.recv(source=rank+1, tag=2)
            for i in range(GRIDSIZE):
                u[my_j_max+1][i+1] = recvbuf[i]

    else:
        # Ranks with even number receive first

        if rank != 0:
            # Receive data from rank-1 (if I'm not the first rank)
            recvbuf = MPI.COMM_WORLD.recv(source=rank-1, tag=1)
            for i in range(GRIDSIZE):
                u[0][i+1] = recvbuf[i]

            # Send data down to rank-1
            for i in range(GRIDSIZE):
                sendbuf[i] = unew[1][i+1]
            MPI.COMM_WORLD.send(sendbuf, dest=rank-1, tag=2)

        if rank != (n_ranks-1):
            # Receive data from rank+1 (if I'm not the last rank)
            recvbuf = MPI.COMM_WORLD.recv(source=rank+1, tag=1)
            for i in range(GRIDSIZE):
                u[my_j_max+1][i+1] = recvbuf[i]

            # Send data up to rank+1
            for i in range(GRIDSIZE):
                sendbuf[i] = unew[my_j_max][i+1]
            MPI.COMM_WORLD.send(sendbuf, dest=rank+1, tag=2)

    # Return the sum over all ranks
    return global_unorm

Optimise

Now it’s time to think about optimising the code. Try it with a different numbers of ranks, up to the maximum number you expect to use. In the next lesson we will talk about a parallel profiler that can produce useful information for this.

It’s also good to check the speed with just one rank. In most cases it can be made as fast as a serial code using the same algorithm.

When making changes to improve performance, keep running the test suite. There is no reason to write a program that is fast but produces wrong results.

Strong Scaling

Strong scaling means increasing the number of ranks without changing the problem. An algorithm with good strong scaling behaviour allows you to solve a problem more and more quickly by throwing more cores at it. There are no real problems where you can achieve perfect strong scaling but some do get close.

Modify the main function to call the poisson_step 100 times and set GRIDSIZE=512.

Try running your program with an increasing number of ranks. Measure the time taken using the Unix time utility. What are the limitations on scaling?

Solution

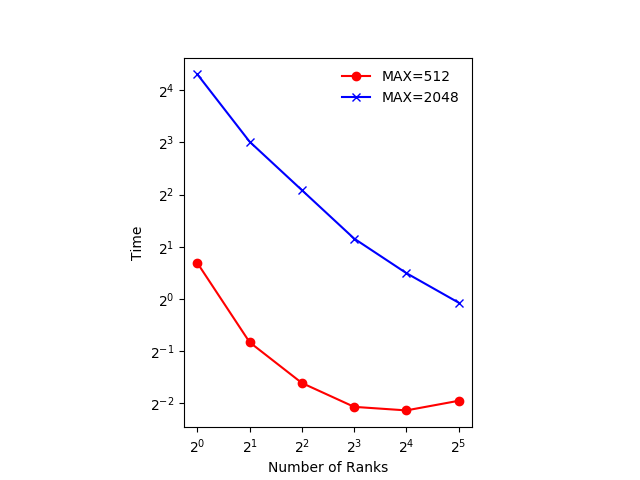
Exact numbers depend on the machine you’re running on, but with a small number of ranks (up to 4) you should see the time decrease with the number of ranks. At 8 ranks the result is a bit worse and doubling again to 16 has little effect.

The figure below shows an example of the scaling with GRIDSIZE=512 and GRIDSIZE=2048.

In the example, which runs on a machine with two 20-core Intel Xeon Scalable CPUs, using 32 ranks actually takes more time. The 32 ranks don’t fit on one CPU and communicating between the the two CPUs takes more time, even though they are in the same machine.

The communication could be made more efficient. We could use non-blocking communication and do some of the computation while communication is happening.

Weak Scaling

Weak scaling refers to increasing the size of the problem while increasing the number of ranks. This is much easier than strong scaling and there are several algorithms with good weak scaling. In fact our algorithm for integrating the Poisson equation might well have perfect weak scaling.

Good weak scaling allows you to solve much larger problems using HPC systems.

Run the Poisson solver with and increasing number of ranks, increasing GRIDSIZE only in the j direction with the number of ranks. How does it behave?

Solution

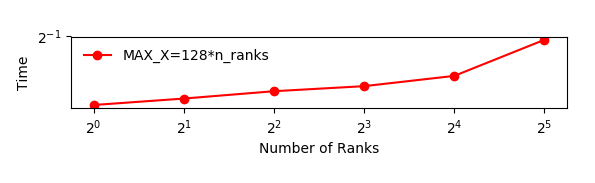
Depending on the machine you’re running on, the runtime should be relatively constant. Runtime increase if you need to use nodes that are further away from each other in the network.

The figure below shows an example of the scaling with GRIDSIZE=128*n_ranks. This is quickly implemented by settings my_j_max to 128.

In this case all the ranks are running on the same node with 40 cores. The increase in runtime is probably due to the memory bandwidth of the node being used by a larger number of cores.

Key Points

Start from a working serial code.

Write a parallel implementation for each function or parallel region.

Connect the parallel regions with a minimal amount of communication.

Continuously compare with the working serial code.

previous episode

Introduction to Parallel Programming with MPI

next episode

Serial to Parallel

Overview

Going from Serial to Parallel

Parallel Regions

Parallel Regions

Solution

Communication Patterns

Communications Patterns

Solution

Set Up Tests

Automated Testing

Write a Test

Solution

Solution

Solution

Make the test work in parallel

Solution

Solution

Solution

Write a Parallel Function Thinking About a Single Rank

Parallel Execution

Solution

Solution

Solution

Communication

Solution

Solution

Solution

Optimise

Strong Scaling

Solution

Weak Scaling

Solution

Key Points

previous episode

next episode